√画像をダウンロード 分数割る整数の仕方 605017

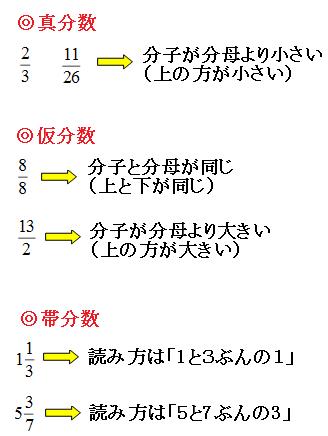
帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説
今回は分数の計算の1つ、分数の足し算のやり方と問題のとき方について書いていきたいと思います。 分数の足し算のやり方 ①分母をそろえる ②分子どうしを足す ③約分する 分母が同じ分数の足し算のやり方 分母が違う分数の足し算のやり方 分数の足し算に関する問題 問題① 問題② 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。
分数割る整数の仕方
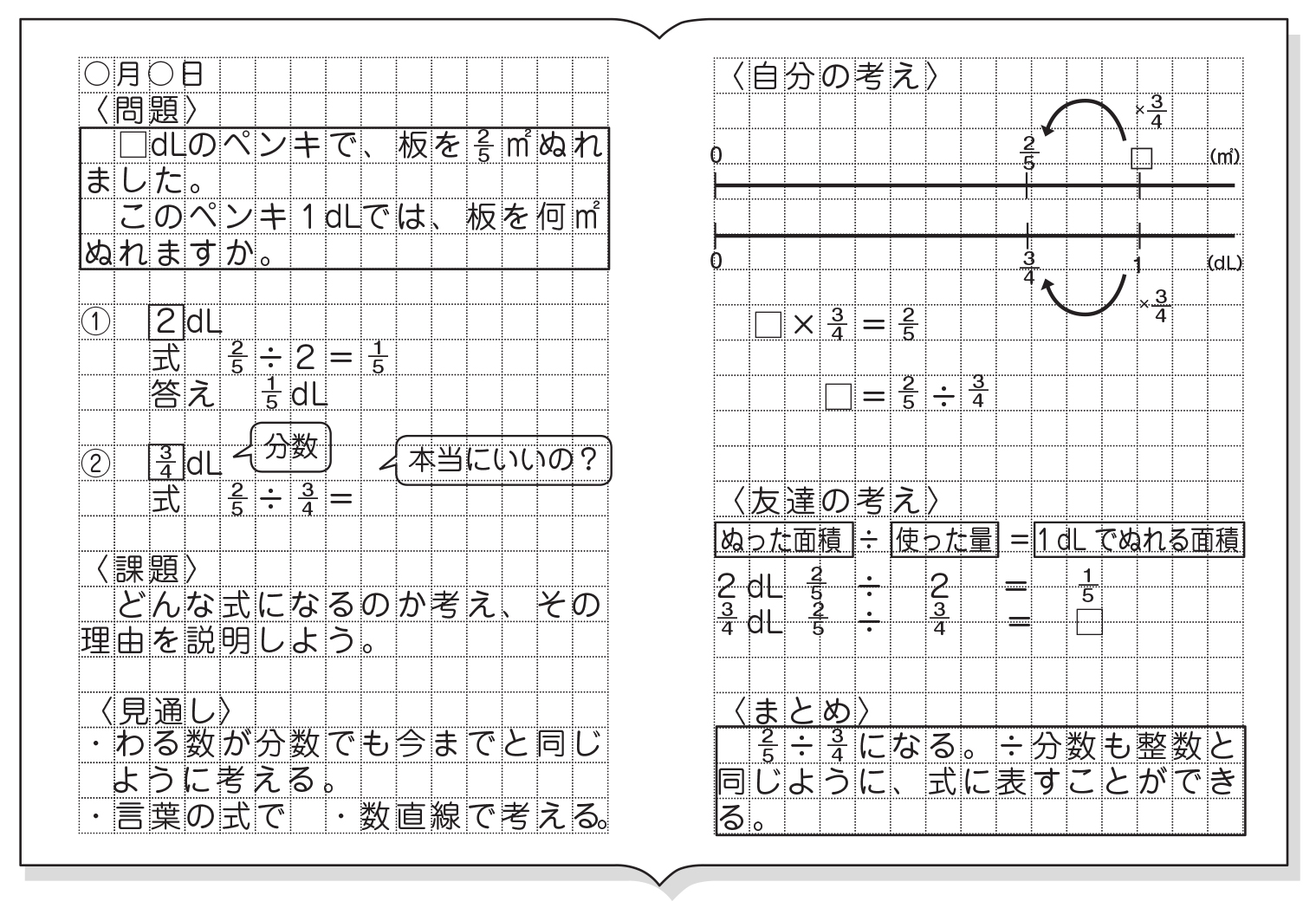
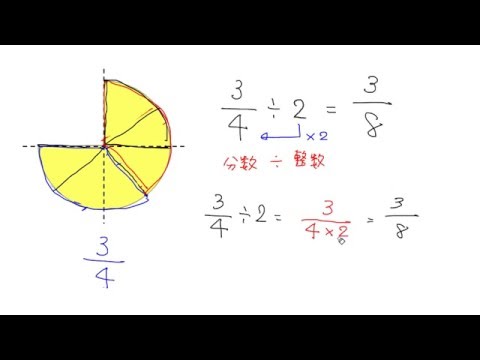
分数割る整数の仕方-5年 分数のわり算 分数÷整数 ねらい 分数でわることの意味と,真分数÷整数の計算の仕方を考え,その計算ができる。 課 題 既 の習 想事 起項 指導上の留意点 自 力 解 決 1 自分の考えを発表する。 集 団 2 かんたんに計算するやり方について話し合う・その23_分数のわり算・整数を分数でわる 6年 「・その22_整数に分数をかける」の次は「整数を分数でわる」。分数計算の基本はこれでおしまいです。 がんばって理解してくださいね。 約分練習の重要性は言うまでもありませんね。

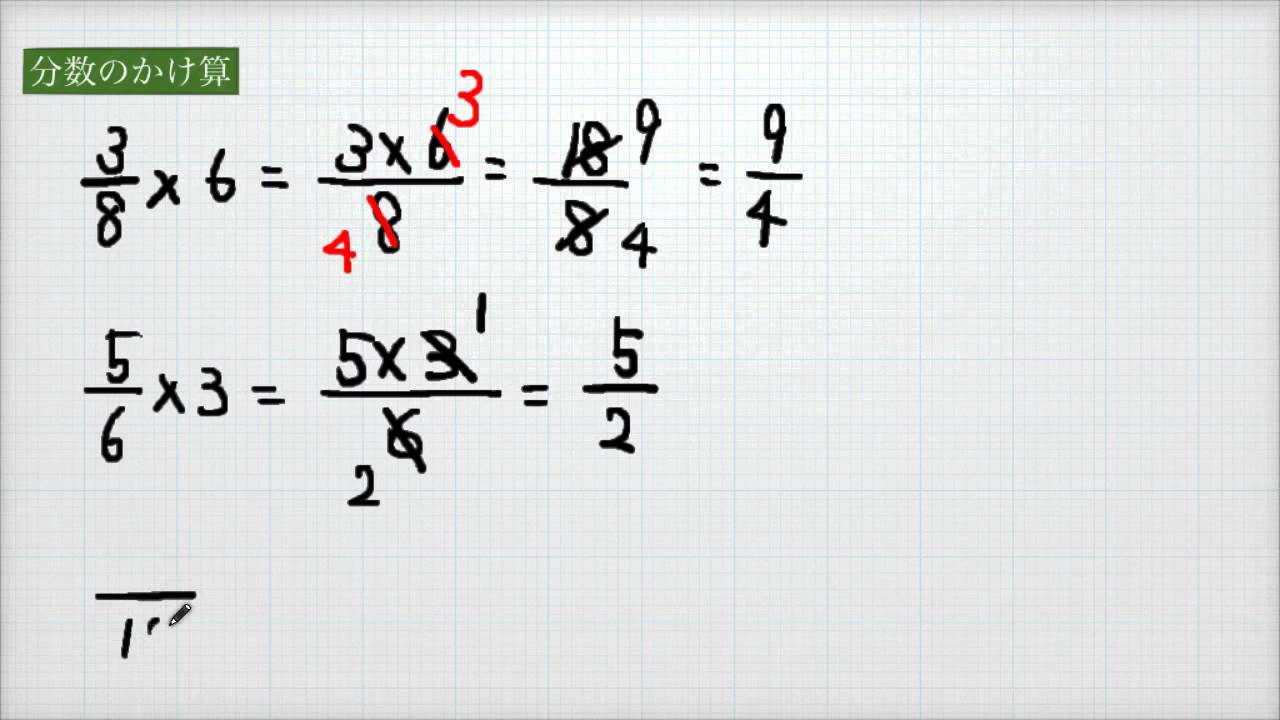
分数のかけ算の問題 やり方は簡単だが 約分に気をつけよう 中学や高校の数学の計算問題
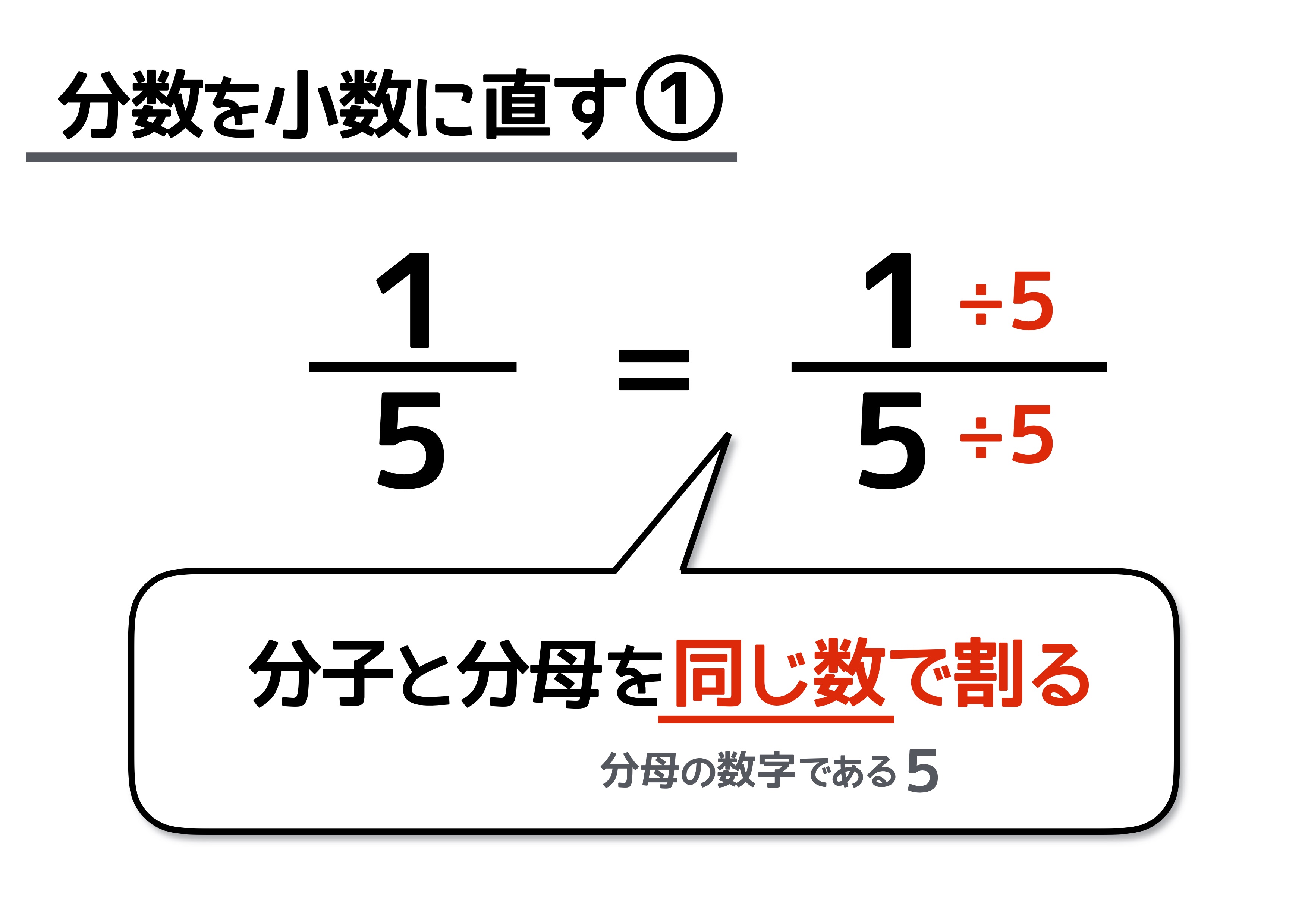
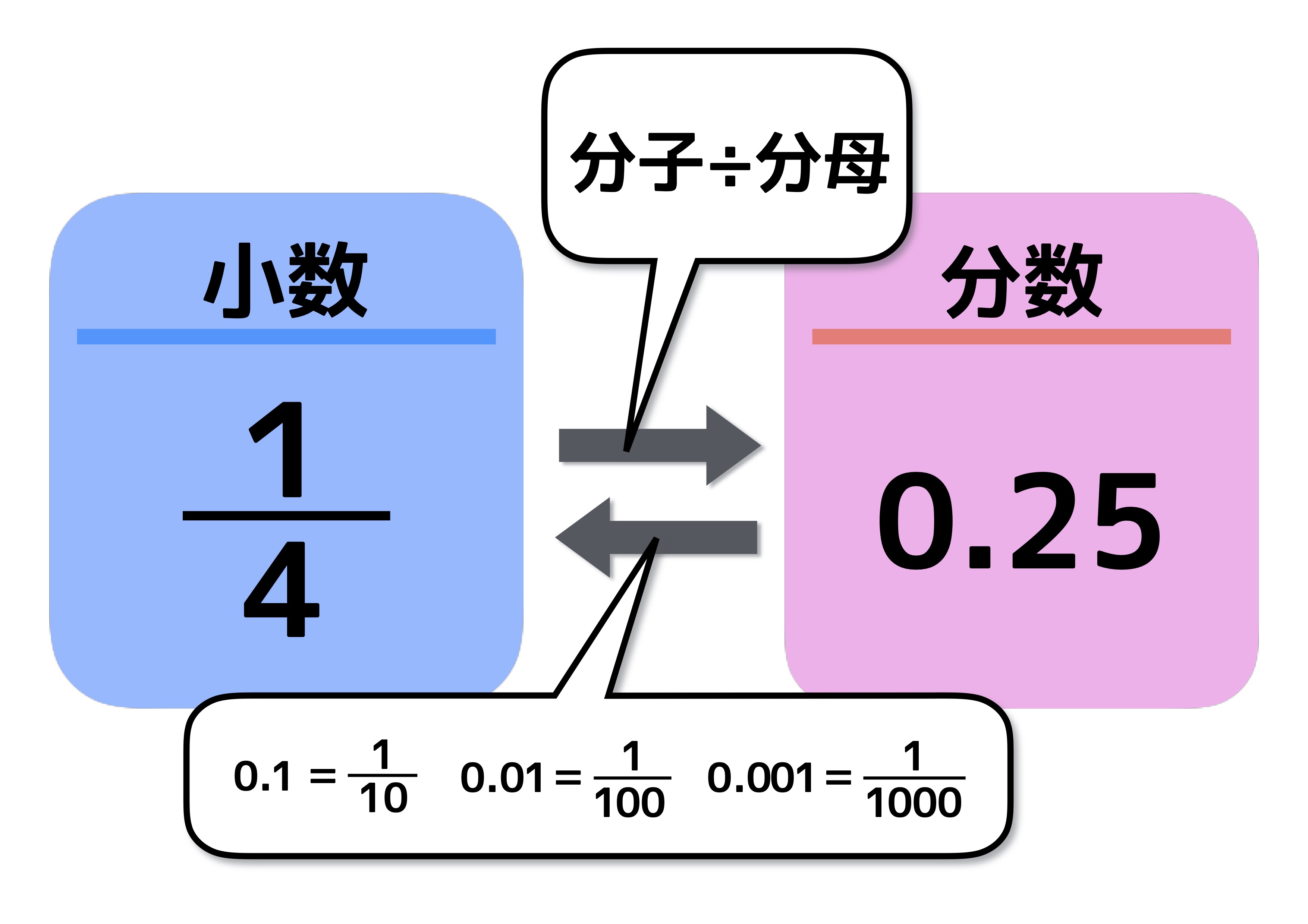
6年 分数のかけ算 6年 分数のわり算 以下は参考のために残してあるページです ① 分数×整数、分数÷整数の意味 ② 分数×整数、分数÷整数の計算 ③ 分数を小数で表すしかた ④ 小数を分数で表すしかた フリー素材提供 教え方1基本 分数 分数とは 分数とは、「1つの物を、何個に切ったうちの何個分」と表すことができる数字です。はじめのうちは、分数が出てくるたびに「何個に切ったうちの何個分」と頭の中で考えて、だいたいどれくらいの大きさの数なのか想像するようにしましょう。割る数が整数だった場合は、整数を分数に直して、それからひっくりかえせば良いのです。 簡単ですね。 分数と整数の割り算 整数の逆数は、まず整数を分数に直してから分母と分子をひっくり返します。 1 5 ÷ 3 ※3を分数にすると、 3 1 3 1 の逆数は 1 3
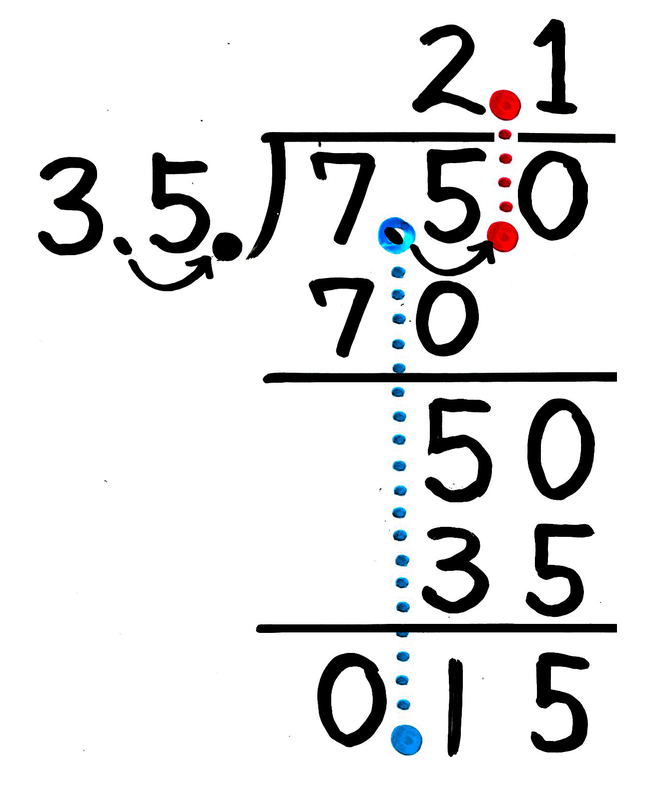
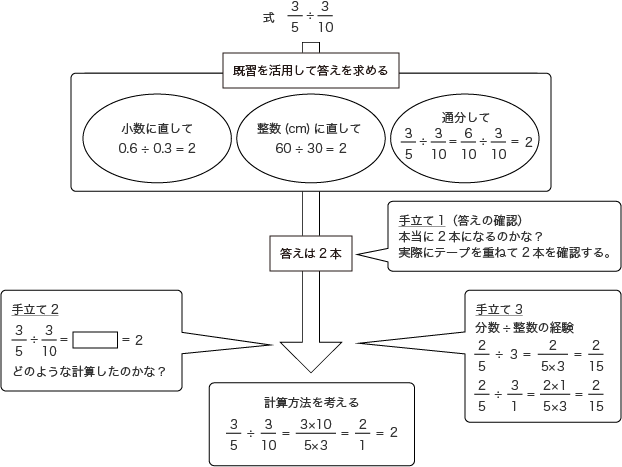
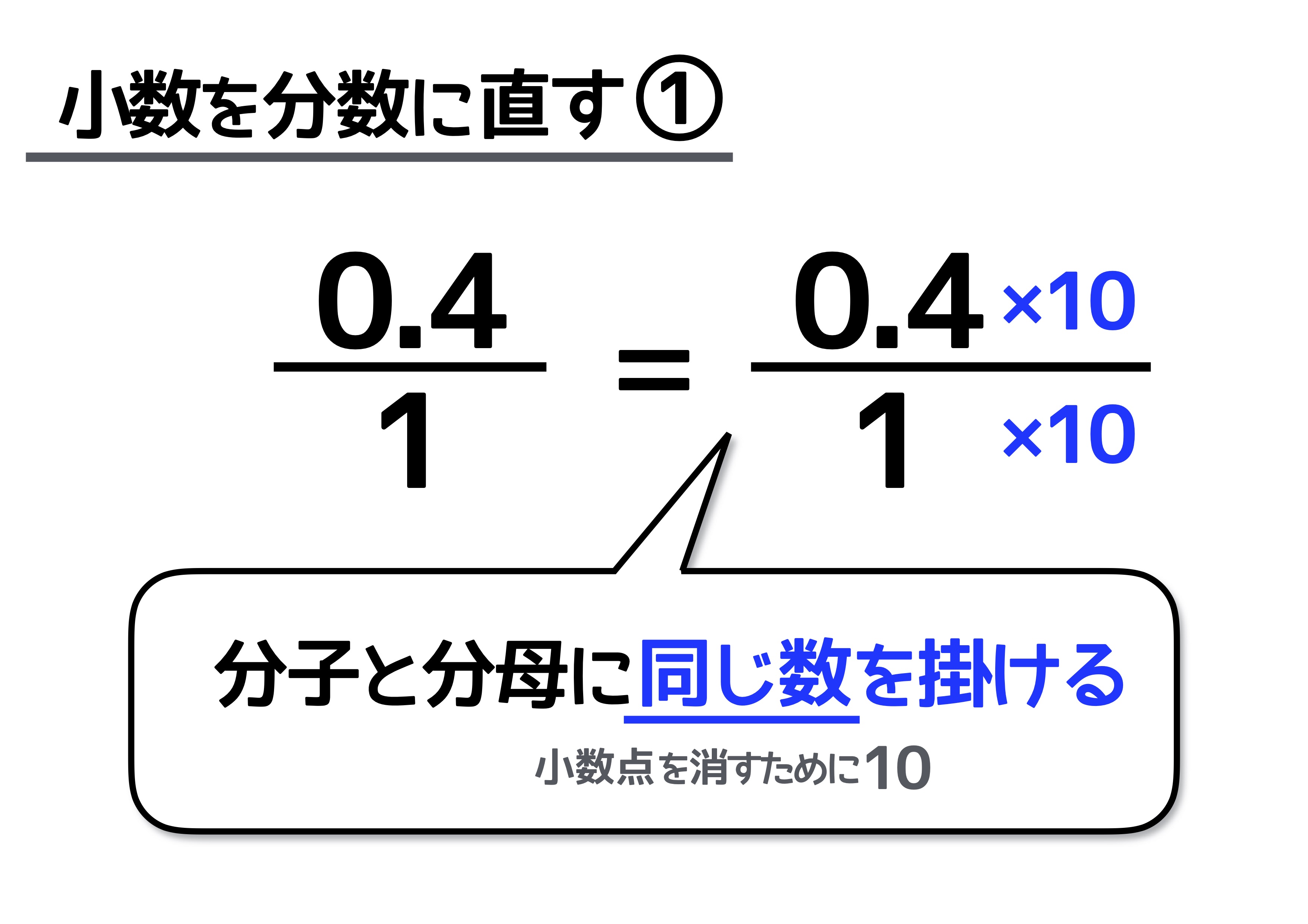
分数×整数 分数×分数 ≪逆数≫ 分数÷整数 分数÷分数 これを見てわかるように、大日本図書 は他の3社と異なり、分数と整数の乗除 をやってから、分数と分数の乗除を載せ ている。また大阪書籍は、逆数をかけ算 とわり算の間に入れ、分数のわり算で割られる数の6に10かけて60、割る数の2に10かけて 両方に同じ数かければ、答えは変わらないのです。 小数点を動かすのは、両方を10倍しているから これを計算する時、小数があると計算しにくい。 だから、小数をなくしてしまえばいい。帯分数の四則演算の解き方 足し算の解き方 帯分数の足し算については、通常の分数の足し算でも重要になる"通分"や帯分数の基本である「\(1\dfrac {2}{3}\)が\(1\dfrac {2}{3}\)であること」などが理解できていれば問題なく計算できるはずです。 では具体的に計算方法について見ていきましょう。
分数割る整数の仕方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
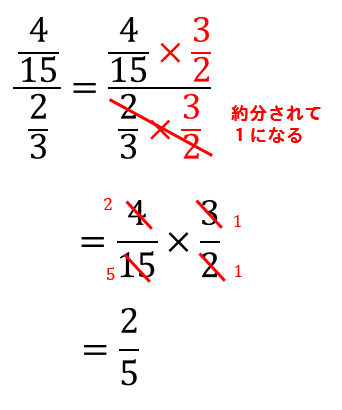 |  | |
 |  |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
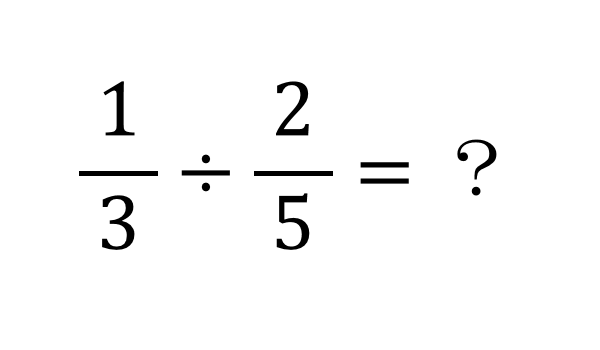 |  | |
 |  |  |
 | 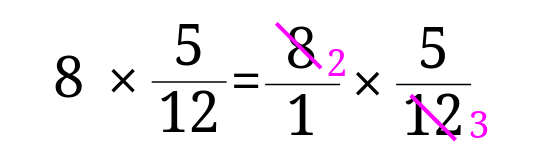 |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 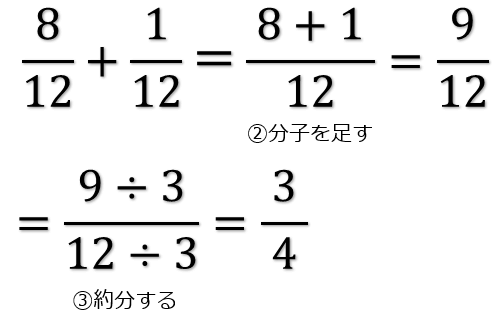 | |
 |  | |
 |  | 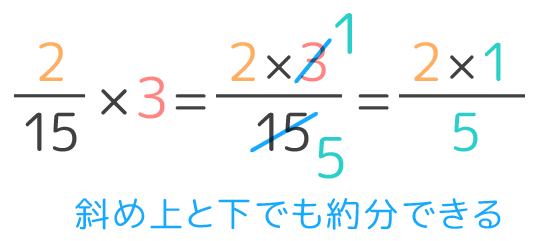 |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
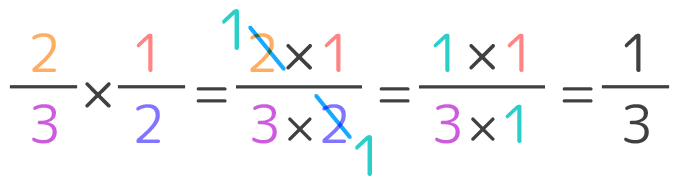 | 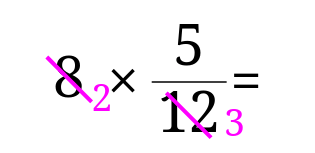 | |
 |  | |
 |  |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
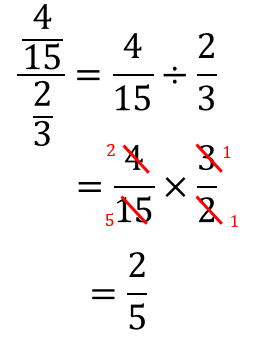 |  | |
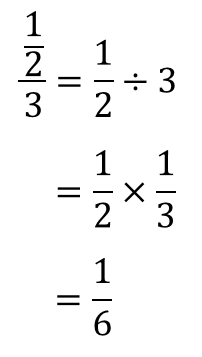 | ||
 |  |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「分数割る整数の仕方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 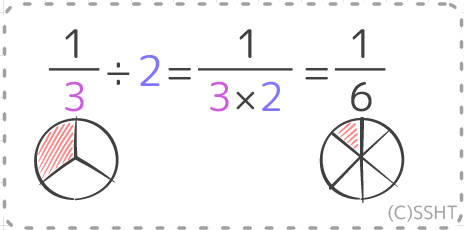 | |
 |
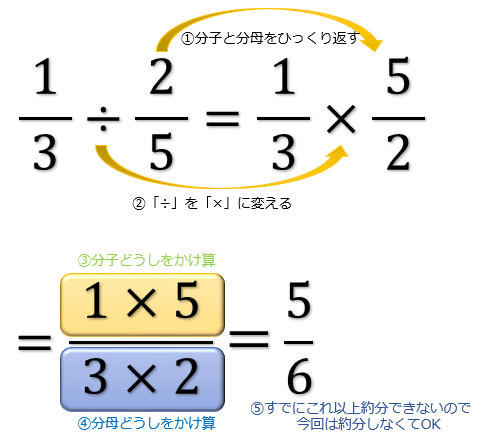
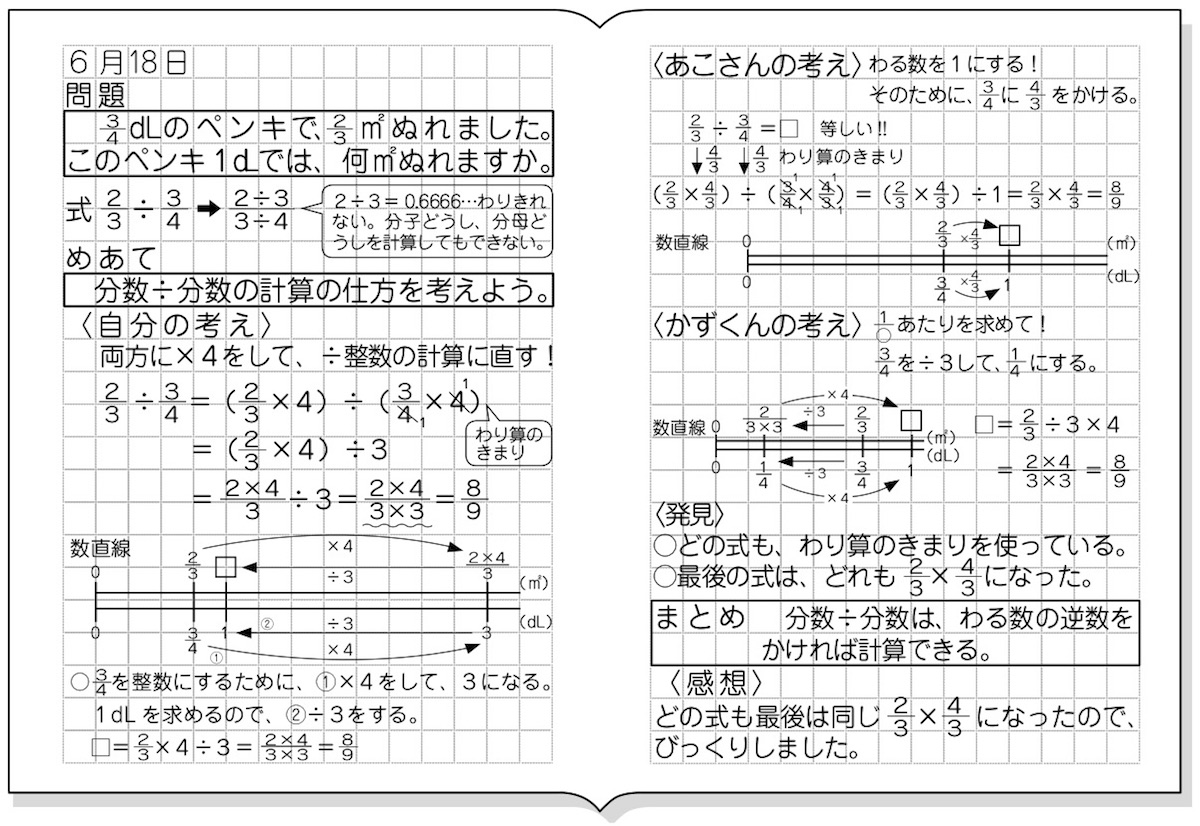
こうすると本来の割る数(ここでは\(\dfrac {3}{4}\))が1になるため、 結局割られる数に割る数の逆数をかける計算になるのです。 小学生でも知っている知識で教えるならこれが最も納得してもらいやすいかと思います。分数÷整数 の計算 分数÷整数の計算も、割る数を逆数にして掛けるという考え方は変わりません。整数は分母が 1 の分数とみなすことができるので、その逆数は ~分の 1 の形になることを確認しておき
コメント
コメントを投稿